| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 (Before Exercise 7.1) | Exercise 7.1 | Example 2 to 9 (Before Exercise 7.2) |
| Exercise 7.2 | ||
Chapter 7 Congruence of Triangles
Welcome to the solutions guide for Chapter 7: Congruence of Triangles. This chapter introduces a fundamental concept in geometry: congruence. In simple terms, two geometric figures are congruent if they are exact duplicates of each other – having precisely the same shape and the same size. Imagine being able to superimpose one figure perfectly onto the other; if they match exactly, they are congruent. While congruence applies to any geometric shapes (like line segments, angles, or other polygons), this chapter focuses specifically on the conditions under which two triangles can be declared congruent. Understanding congruence is vital as it forms the basis for proving many other geometric properties and theorems.
The solutions page meticulously explains that congruence between two triangles, say $\triangle ABC$ and $\triangle PQR$, implies a very specific one-to-one correspondence between their parts. This means:
- Their corresponding vertices match up: $A \leftrightarrow P$, $B \leftrightarrow Q$, $C \leftrightarrow R$.
- Their corresponding sides are equal in length: $\overline{AB} = \overline{PQ}$, $\overline{BC} = \overline{QR}$, $\overline{CA} = \overline{RP}$.
- Their corresponding angles are equal in measure: $\angle A = \angle P$, $\angle B = \angle Q$, $\angle C = \angle R$.
If all six of these corresponding parts (3 sides, 3 angles) are equal, the triangles are congruent. However, we don't need to check all six parts! The core of this chapter revolves around establishing the minimum conditions, known as Congruence Criteria (or rules/postulates), that are sufficient to guarantee congruence.
The solutions detail the four primary criteria for triangle congruence:
- SSS (Side-Side-Side) Criterion: If the three sides of one triangle are equal to the three corresponding sides of another triangle, then the two triangles are congruent. (If $AB=PQ, BC=QR, CA=RP$, then $\triangle ABC \cong \triangle PQR$).
- SAS (Side-Angle-Side) Criterion: If two sides and the included angle (the angle formed *between* those two sides) of one triangle are equal to the corresponding two sides and the included angle of another triangle, then the two triangles are congruent. (If $AB=PQ, \angle B = \angle Q, BC=QR$, then $\triangle ABC \cong \triangle PQR$). Crucially, the angle must be the one included between the two sides.
- ASA (Angle-Side-Angle) Criterion: If two angles and the included side (the side *between* those two angles) of one triangle are equal to the corresponding two angles and the included side of another triangle, then the two triangles are congruent. (If $\angle B = \angle Q, BC=QR, \angle C = \angle R$, then $\triangle ABC \cong \triangle PQR$). Crucially, the side must be the one included between the two angles.
- RHS (Right angle-Hypotenuse-Side) Criterion: This criterion applies specifically to right-angled triangles. If the hypotenuse and one corresponding side (leg) of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, then the two triangles are congruent. (If $\triangle ABC$ and $\triangle PQR$ are right-angled at B and Q respectively, and Hypotenuse $AC=$ Hypotenuse $PR$, and Side $BC=$ Side $QR$, then $\triangle ABC \cong \triangle PQR$).
For each criterion, the solutions provide numerous examples. Students are guided through examining diagrams, identifying given equal parts (often indicated by markings or stated facts), determining if one of the SSS, SAS, ASA, or RHS conditions is met, and then writing the formal congruence statement. Strong emphasis is placed on the correct symbolic notation, such as $\triangle ABC \cong \triangle PQR$. The order of the vertices in this statement is critical, as it explicitly defines the correspondence: $A \leftrightarrow P$, $B \leftrightarrow Q$, and $C \leftrightarrow R$. Writing $\triangle ABC \cong \triangle QRP$ would imply a different correspondence and would likely be incorrect if the previous matching was intended.
Once congruence is established using one of these criteria, the solutions introduce the powerful principle often abbreviated as CPCTC: Corresponding Parts of Congruent Triangles are Congruent (or equal). This means that after proving $\triangle ABC \cong \triangle PQR$ using, say, SAS, we can automatically conclude that the remaining corresponding parts are also equal ($\angle A = \angle P$, $\angle C = \angle R$, and $AC = PR$) without further measurement or proof. This principle is fundamental for solving problems that require finding unknown angles or sides, or for performing simple geometric proofs. The solutions demonstrate this logical deduction process, thereby enhancing deductive reasoning skills crucial for future geometry studies.
Example 1 (Before Exercise 7.1)
Example 1 ∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) $\overline{PQ}$
(ii) ∠Q
(iii) $\overline{RP}$
Answer:
Given:
The congruence correspondence between the two triangles is given as:
ABC ↔ RQP
This correspondence tells us which vertices match up. By comparing the positions of the letters, we can identify the corresponding parts:
- Vertex A corresponds to Vertex R (A ↔ R)
- Vertex B corresponds to Vertex Q (B ↔ Q)
- Vertex C corresponds to Vertex P (C ↔ P)
(i) Find the part corresponding to $\overline{PQ}$
The line segment $\overline{PQ}$ is formed by the vertices P and Q.
From our correspondence:
Vertex P corresponds to Vertex C.
Vertex Q corresponds to Vertex B.
Therefore, the side $\overline{PQ}$ corresponds to the side $\overline{CB}$.
(ii) Find the part corresponding to ∠Q
The angle ∠Q is at vertex Q.
From our correspondence, the middle vertex Q corresponds to the middle vertex B.
Therefore, the angle ∠Q corresponds to the angle ∠B.
(iii) Find the part corresponding to $\overline{RP}$
The line segment $\overline{RP}$ is formed by the vertices R and P.
From our correspondence:
Vertex R corresponds to Vertex A.
Vertex P corresponds to Vertex C.
Therefore, the side $\overline{RP}$ corresponds to the side $\overline{AC}$.
Exercise 7.1
Question 1. Complete the following statements:
(a) Two line segments are congruent if ___________.
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is ___________.
(c) When we write ∠A = ∠B, we actually mean ___________.
Answer:
Here are the completed statements:
(a) Two line segments are congruent if they have the same length.
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is 70°.
(Congruent angles have the same measure).
(c) When we write ∠A = ∠B, we actually mean m∠A = m∠B (i.e., the measure of angle A is equal to the measure of angle B).
Question 2. Give any two real-life examples for congruent shapes.
Answer:
Congruent shapes are shapes that are exactly the same size and shape. If you can place one shape on top of the other and they match perfectly, they are congruent.
Here are two real-life examples of congruent shapes:
1. Two copies of the same photograph printed from the same negative or digital file without resizing.
2. Blades of the same fan (assuming it's a well-manufactured fan).
Other examples include:
- Biscuits from the same packet.
- Sheets of paper from the same ream.
- Coins of the same denomination from the same mint and year.
- Matching pairs of shoes.
- Keys made from the same mould.
Question 3. If ∆ABC ≅ ∆FED under the correspondence ABC ↔ FED, write all the corresponding congruent parts of the triangles.
Answer:
Given:
The two triangles are congruent, which is given by the statement $\triangle ABC \cong \triangle FED$.
The correspondence is given as ABC ↔ FED. This tells us which vertices, angles, and sides match up between the two triangles.
The correspondence of vertices is as follows:
A ↔ F
B ↔ E
C ↔ D
Since the triangles are congruent, their corresponding parts must also be congruent. Based on the vertex correspondence, we can list all the congruent parts.
Corresponding Congruent Angles:
1. The angle at vertex A corresponds to the angle at vertex F. So, $\angle A \cong \angle F$.
2. The angle at vertex B corresponds to the angle at vertex E. So, $\angle B \cong \angle E$.
3. The angle at vertex C corresponds to the angle at vertex D. So, $\angle C \cong \angle D$.
Corresponding Congruent Sides:
1. The side between vertices A and B corresponds to the side between F and E. So, $\overline{AB} \cong \overline{FE}$.
2. The side between vertices B and C corresponds to the side between E and D. So, $\overline{BC} \cong \overline{ED}$.
3. The side between vertices C and A corresponds to the side between D and F. So, $\overline{CA} \cong \overline{DF}$.
Question 4. If ∆DEF ≅ ∆BCA, write the part(s) of ∆BCA that correspond to
(i) ∠E
(ii) $\overline{EF}$
(iii) ∠F
(iv) $\overline{DF}$
Answer:
Given:
The congruence of the two triangles is given as $\triangle DEF \cong \triangle BCA$.
The correspondence between the vertices is DEF ↔ BCA. This means:
D ↔ B
E ↔ C
F ↔ A
We can use this correspondence to find the matching parts of $\triangle BCA$.
(i) The part of $\triangle BCA$ that corresponds to $\angle E$:
From the correspondence, vertex E matches with vertex C.
Therefore, $\angle E$ corresponds to $\angle C$.
(ii) The part of $\triangle BCA$ that corresponds to $\overline{EF}$:
The side $\overline{EF}$ is formed by vertices E and F.
From the correspondence, E matches with C, and F matches with A.
Therefore, $\overline{EF}$ corresponds to $\overline{CA}$.
(iii) The part of $\triangle BCA$ that corresponds to $\angle F$:
From the correspondence, vertex F matches with vertex A.
Therefore, $\angle F$ corresponds to $\angle A$.
(iv) The part of $\triangle BCA$ that corresponds to $\overline{DF}$:
The side $\overline{DF}$ is formed by vertices D and F.
From the correspondence, D matches with B, and F matches with A.
Therefore, $\overline{DF}$ corresponds to $\overline{BA}$.
Example 2 to 9 (Before Exercise 7.2)
Example 2 In triangles ABC and PQR, AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm. Examine whether the two triangles are congruent or not. If yes, write the congruence relation in symbolic form.
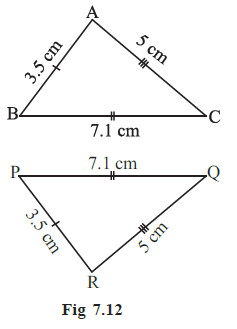
Answer:
Given:
In $\triangle ABC$:
AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm
In $\triangle PQR$:
PQ = 7.1 cm, QR = 5 cm, PR = 3.5 cm
Solution:
To examine if the triangles are congruent, we compare the lengths of their sides to find corresponding equal parts.
AB = 3.5 cm and PR = 3.5 cm
$\implies$ AB = PR
BC = 7.1 cm and PQ = 7.1 cm
$\implies$ BC = PQ
AC = 5 cm and QR = 5 cm
$\implies$ AC = QR
Since all three sides of $\triangle ABC$ are equal to the corresponding three sides of $\triangle PQR$, the triangles are congruent by the SSS (Side-Side-Side) congruence criterion.
Writing the Congruence Relation:
To write the relation in symbolic form, we need to find the correct correspondence of the vertices.
Side AB corresponds to side PR. So, vertex A corresponds to R and vertex B corresponds to P. (A ↔ R, B ↔ P)
Side BC corresponds to side PQ. So, vertex B corresponds to P and vertex C corresponds to Q. (B ↔ P, C ↔ Q)
Side AC corresponds to side QR. So, vertex A corresponds to R and vertex C corresponds to Q. (A ↔ R, C ↔ Q)
Combining these, we get the correspondence:
A ↔ R
B ↔ P
C ↔ Q
Thus, the congruence can be written as:
$\triangle ABC \cong \triangle RPQ$
Example 3 In Fig 7.13, AD = CD and AB = CB.
(i) State the three pairs of equal parts in ∆ABD and ∆CBD.
(ii) Is ∆ABD ≅ ∆CBD? Why or why not?
(iii) Does BD bisect ∠ABC? Give reasons.
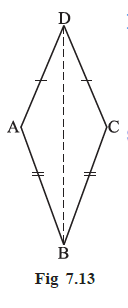
Answer:
Given:
AD = CD
AB = CB
Solution:
(i) State the three pairs of equal parts in $\triangle ABD$ and $\triangle CBD$.
The three pairs of equal parts are:
AB = CB
(Given)
AD = CD
(Given)
BD = BD
(Common side)
(ii) Is $\triangle ABD \cong \triangle CBD$? Why or why not?
Yes, $\triangle ABD \cong \triangle CBD$.
Reason: The two triangles satisfy the SSS (Side-Side-Side) congruence criterion because all three corresponding sides are equal, as shown in part (i).
(iii) Does BD bisect $\angle ABC$? Give reasons.
Yes, BD bisects $\angle ABC$.
Reason: Since we have proved that $\triangle ABD \cong \triangle CBD$, their corresponding parts must be equal. This is known as CPCT (Corresponding Parts of Congruent Triangles).
The angle $\angle ABD$ in $\triangle ABD$ corresponds to the angle $\angle CBD$ in $\triangle CBD$.
Therefore, $\angle ABD = \angle CBD$ (by CPCT). Since the line segment BD divides $\angle ABC$ into two equal angles, it bisects the angle.
Example 4 Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using SAS congruence rule. If the triangles are congruent, write them in symbolic form.
∆ABC
(a) AB = 7 cm, BC = 5 cm, ∠B = 50°
(b) AB = 4.5 cm, AC = 4 cm, ∠A = 60°
(c) BC = 6 cm, AC = 4 cm, ∠B = 35°
∆DEF
(i) DE = 5 cm, EF = 7 cm, ∠E = 50°
(ii) DE = 4 cm, FD = 4.5 cm, ∠D = 55°
(iii) DF = 4 cm, EF = 6 cm, ∠E = 35°
(It will be always helpful to draw a rough figure, mark the measurements and then probe the question).
Answer:
The SAS (Side-Angle-Side) congruence rule states that two triangles are congruent if two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of the other triangle.
Case (a) and (i)
Given:
In $\triangle ABC$: AB = 7 cm, BC = 5 cm, $\angle B = 50^\circ$.
In $\triangle DEF$: DE = 5 cm, EF = 7 cm, $\angle E = 50^\circ$.
Comparison:
Side AB (7 cm) = Side EF (7 cm).
Side BC (5 cm) = Side DE (5 cm).
The angle included between sides AB and BC is $\angle B = 50^\circ$.
The angle included between sides EF and DE is $\angle E = 50^\circ$.
Since AB = EF, BC = DE, and the included angle $\angle B = \angle E$, the SAS condition is met.
Conclusion: The triangles are congruent. The correspondence is A↔F, B↔E, C↔D. So, $\triangle ABC \cong \triangle FED$.
Case (b) and (ii)
Given:
In $\triangle ABC$: AB = 4.5 cm, AC = 4 cm, $\angle A = 60^\circ$.
In $\triangle DEF$: DE = 4 cm, FD = 4.5 cm, $\angle D = 55^\circ$.
Comparison:
Side AB (4.5 cm) = Side FD (4.5 cm).
Side AC (4 cm) = Side DE (4 cm).
The included angle between AB and AC is $\angle A = 60^\circ$.
The included angle between FD and DE is $\angle D = 55^\circ$.
Since $\angle A \neq \angle D$ ($60^\circ \neq 55^\circ$), the SAS condition is not met.
Conclusion: The triangles are not congruent.
Case (c) and (iii)
Given:
In $\triangle ABC$: BC = 6 cm, AC = 4 cm, $\angle B = 35^\circ$.
In $\triangle DEF$: DF = 4 cm, EF = 6 cm, $\angle E = 35^\circ$.
Comparison:
Side BC (6 cm) = Side EF (6 cm).
Side AC (4 cm) = Side DF (4 cm).
In $\triangle ABC$, the given angle is $\angle B = 35^\circ$. This angle is not included between the sides BC and AC (the included angle would be $\angle C$).
In $\triangle DEF$, the given angle is $\angle E = 35^\circ$. This angle is also not included between the sides EF and DF (the included angle would be $\angle F$).
Since the given equal angle is not the included angle in both triangles, the SAS criterion cannot be applied.
Conclusion: The triangles are not congruent by the SAS rule.
Example 5 In Fig 7.23, AB = AC and AD is the bisector of ∠BAC.
(i) State three pairs of equal parts in triangles ADB and ADC.
(ii) Is ∆ADB ≅ ∆ADC? Give reasons.
(iii) Is ∠B = ∠C? Give reasons.
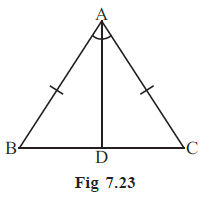
Answer:
Given:
AB = AC
AD bisects $\angle BAC$
Solution:
(i) State three pairs of equal parts in triangles ADB and ADC.
Consider $\triangle ADB$ and $\triangle ADC$. The three pairs of equal parts are:
AB = AC
(Given)
$\angle BAD = \angle CAD$
(AD bisects $\angle BAC$)
AD = AD
(Common side)
(ii) Is $\triangle ADB \cong \triangle ADC$? Give reasons.
Yes, $\triangle ADB \cong \triangle ADC$.
Reason: We have established two equal sides (AB = AC and AD = AD) and the included angle ($\angle BAD = \angle CAD$) between them is also equal. This satisfies the SAS (Side-Angle-Side) congruence criterion.
(iii) Is $\angle B = \angle C$? Give reasons.
Yes, $\angle B = \angle C$.
Reason: Since $\triangle ADB \cong \triangle ADC$, their corresponding parts must be equal (by CPCT). The angle at vertex B ($\angle B$) in $\triangle ADB$ corresponds to the angle at vertex C ($\angle C$) in $\triangle ADC$. Therefore, $\angle B = \angle C$.
Example 6 By applying ASA congruence rule, it is to be established that ∆ABC ≅∆QRP and it is given that BC = RP. What additional information is needed to establish the congruence?
Answer:
Given:
We need to prove $\triangle ABC \cong \triangle QRP$ using the ASA congruence rule.
We are given one pair of equal sides: BC = RP.
Solution:
The ASA (Angle-Side-Angle) congruence rule requires two angles and the included side of one triangle to be equal to the corresponding parts of another triangle.
We are given the side BC = RP. For the ASA rule to apply, this side must be the included side between two angles.
In $\triangle ABC$, the side BC is included between $\angle B$ and $\angle C$.
In $\triangle QRP$, the side RP is included between $\angle R$ and $\angle P$.
The congruence we want to establish is $\triangle ABC \cong \triangle QRP$. This implies the correspondence:
A ↔ Q
B ↔ R
C ↔ P
For the ASA criterion to be satisfied with this correspondence, the angles at the endpoints of the given equal sides must also correspond and be equal.
1. The angle at vertex B must be equal to the angle at its corresponding vertex R. So, we need $\angle B = \angle R$.
2. The angle at vertex C must be equal to the angle at its corresponding vertex P. So, we need $\angle C = \angle P$.
Therefore, the additional information needed is:
$\angle B = \angle R$ and $\angle C = \angle P$.
Example 7 In Fig 7.26, can you use ASA congruence rule and conclude that ∆AOC ≅ ∆BOD?
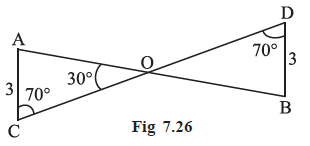
Answer:
Given Information from the Figure:
In $\triangle AOC$:
$\angle CAO = 30^\circ$
$\angle ACO = 70^\circ$
AC = 3
In $\triangle BOD$:
$\angle BDO = 70^\circ$
BD = 3
To Examine:
Can we use the ASA congruence rule to conclude that $\triangle AOC \cong \triangle BOD$?
Solution:
The ASA (Angle-Side-Angle) congruence criterion states that two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and included side of the other triangle.
First, let's find all the angles of both triangles.
In $\triangle AOC$:
Using the Angle Sum Property of a triangle:
$\angle AOC + \angle CAO + \angle ACO = 180^\circ$
(Angle Sum Property)
$\angle AOC + 30^\circ + 70^\circ = 180^\circ$
$\angle AOC + 100^\circ = 180^\circ$
$\angle AOC = 180^\circ - 100^\circ = 80^\circ$
In $\triangle BOD$:
The angle $\angle BOD$ is vertically opposite to $\angle AOC$.
$\angle BOD = \angle AOC = 80^\circ$
(Vertically opposite angles)
Now, using the Angle Sum Property for $\triangle BOD$:
$\angle OBD + \angle BDO + \angle BOD = 180^\circ$
(Angle Sum Property)
$\angle OBD + 70^\circ + 80^\circ = 180^\circ$
$\angle OBD + 150^\circ = 180^\circ$
$\angle OBD = 180^\circ - 150^\circ = 30^\circ$
Applying the ASA Congruence Rule:
Now we compare the parts of $\triangle AOC$ and $\triangle BOD$ to see if the ASA criterion is met.
In $\triangle AOC$, we have angles $\angle CAO = 30^\circ$ and $\angle ACO = 70^\circ$. The side included between them is AC = 3.
In $\triangle BOD$, we have angles $\angle OBD = 30^\circ$ and $\angle BDO = 70^\circ$. The side included between them is BD = 3.
Let's check the correspondence:
1. Angle: $\angle CAO = \angle OBD = 30^\circ$
2. Included Side: AC = BD = 3
3. Angle: $\angle ACO = \angle BDO = 70^\circ$
Since two angles and the included side of $\triangle AOC$ are equal to the corresponding two angles and included side of $\triangle BOD$, the ASA congruence condition is satisfied.
Conclusion:
Yes, we can use the ASA congruence rule to conclude that the triangles are congruent.
The congruence relation is $\triangle AOC \cong \triangle BOD$.
Example 8 Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, using RHS congruence rule. In case of congruent triangles, write the result in symbolic form:
∆ABC
(i) ∠B = 90°, AC = 8 cm, AB = 3 cm
(ii) ∠A = 90°, AC = 5 cm, BC = 9 cm
∆PQR
(a) ∠P = 90°, PR = 3 cm, QR = 8 cm
(b) ∠Q = 90°, PR = 8 cm, PQ = 5 cm
Answer:
The RHS (Right angle-Hypotenuse-Side) congruence rule applies to right-angled triangles. It states that two right-angled triangles are congruent if the hypotenuse and one side of one triangle are equal to the corresponding hypotenuse and side of the other triangle.
Case (i) and (a)
Given:
In $\triangle ABC$: $\angle B = 90^\circ$, AC = 8 cm, AB = 3 cm
In $\triangle PQR$: $\angle P = 90^\circ$, PR = 3 cm, QR = 8 cm
Let's check the conditions for RHS:
Right Angle (R): $\angle B = 90^\circ$ and $\angle P = 90^\circ$. The condition is met.
Hypotenuse (H): In $\triangle ABC$, the hypotenuse is AC = 8 cm. In $\triangle PQR$, the hypotenuse is QR = 8 cm. So, AC = QR. The condition is met.
Side (S): In $\triangle ABC$, one side is AB = 3 cm. In $\triangle PQR$, one side is PR = 3 cm. So, AB = PR. The condition is met.
Since all three conditions of RHS are satisfied, the triangles are congruent.
Symbolic Form: The correspondence is A↔R (since AB=PR), B↔P (right angles), C↔Q (from hypotenuses AC=QR). Thus, $\triangle ABC \cong \triangle RPQ$.
Case (ii) and (b)
Given:
In $\triangle ABC$: $\angle A = 90^\circ$, AC = 5 cm, BC = 9 cm
In $\triangle PQR$: $\angle Q = 90^\circ$, PR = 8 cm, PQ = 5 cm
Let's check the conditions for RHS:
Right Angle (R): $\angle A = 90^\circ$ and $\angle Q = 90^\circ$. The condition is met.
Hypotenuse (H): In $\triangle ABC$, the hypotenuse is BC = 9 cm. In $\triangle PQR$, the hypotenuse is PR = 8 cm. Since $9 \text{ cm} \neq 8 \text{ cm}$, the hypotenuses are not equal.
Since the hypotenuses are not equal, the RHS criterion is not met.
Conclusion: The triangles are not congruent.
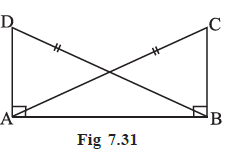
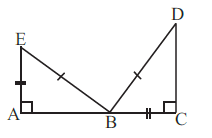
Example 9 In Fig 7.31, DA ⊥AB, CB ⊥ AB and AC = BD. State the three pairs of equal parts in ∆ABC and ∆DAB. Which of the following statements is meaningful?
(i) ∆ABC ≅∆BAD
(ii) ∆ABC ≅∆ABD
Answer:
Given:
In the adjoining figure, we have two triangles, $\triangle ABC$ and $\triangle DAB$.
1. DA $\perp$ AB, which means $\angle DAB = 90^\circ$.
2. CB $\perp$ AB, which means $\angle CBA = 90^\circ$.
3. AC = BD (marked on the figure and given in the text).
To Find:
1. The three pairs of equal parts in $\triangle ABC$ and $\triangle DAB$.
2. Which of the given congruence statements, (i) or (ii), is meaningful.
Solution:
1. Three Pairs of Equal Parts
Let's compare the parts of $\triangle ABC$ and $\triangle DAB$ based on the given information.
$\angle CBA = \angle DAB$
(Both are equal to 90°)
This shows that both triangles are right-angled triangles.
AC = BD
(Given)
In $\triangle ABC$, AC is the side opposite the right angle ($\angle CBA$), so it is the hypotenuse. In $\triangle DAB$, BD is the side opposite the right angle ($\angle DAB$), so it is also the hypotenuse. Thus, the hypotenuses are equal.
AB = BA
(Common side to both triangles)
So, the three pairs of equal parts are a right angle, the hypotenuse, and a corresponding side.
2. Meaningful Congruence Statement
Based on the equal parts identified above, we can see that the conditions for the RHS (Right angle - Hypotenuse - Side) congruence rule are satisfied. Therefore, the triangles are congruent.
To determine the correct symbolic statement, we need to establish the correct correspondence between the vertices.
- The right angle in $\triangle ABC$ is at vertex B. The right angle in $\triangle DAB$ is at vertex A. So, the vertex correspondence is B ↔ A.
- The hypotenuse of $\triangle ABC$ is AC. The hypotenuse of $\triangle DAB$ is BD. Since AC = BD, the endpoints {A, C} correspond to {B, D}. As we already know B ↔ A, it follows that C ↔ D.
- This leaves the remaining vertex A from $\triangle ABC$ to correspond with vertex B from $\triangle DAB$. So, A ↔ B.
The complete correspondence is: ABC ↔ BAD.
Therefore, the correct congruence statement is $\triangle ABC \cong \triangle BAD$.
Now let's check the given options:
(i) $\triangle ABC \cong \triangle BAD$
This statement perfectly matches the correspondence we derived (A↔B, B↔A, C↔D). Hence, this statement is meaningful.
(ii) $\triangle ABC \cong \triangle ABD$
This statement implies the correspondence A↔A, B↔B, C↔D. This is incorrect because the right angle at B in $\triangle ABC$ does not correspond to the angle at B in $\triangle DAB$ ($\angle CBA \neq \angle ABD$). Hence, this statement is not meaningful.
Exercise 7.2
Question 1. Which congruence criterion do you use in the following?
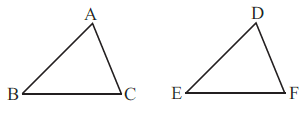
(a) Given:AC = DF
AB = DE
BC = EF
So, ∆ABC ≅ ∆DEF
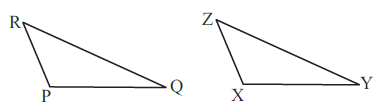
(b) Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆PQR ≅ ∆XYZ
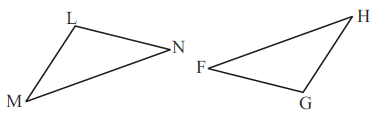
(c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ∆LMN ≅ ∆GFH
(d) Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ∆ABE ≅ ∆CDB
Answer:
(a)
In $\triangle ABC$ and $\triangle DEF$, the following parts are given as equal:
AC = DF
(Side) (Given)
AB = DE
(Side) (Given)
BC = EF
(Side) (Given)
Conclusion: $\triangle ABC \cong \triangle DEF$
Criterion Used:
Since the three sides of $\triangle ABC$ are equal to the corresponding three sides of $\triangle DEF$, the congruence is established by the SSS (Side-Side-Side) congruence criterion.
(b)
In $\triangle PQR$ and $\triangle XYZ$, the following parts are given as equal:
ZX = RP
(Side) (Given)
RQ = ZY
(Side) (Given)
$\angle PRQ = \angle XZY$
(Angle) (Given)
Conclusion: $\triangle PQR \cong \triangle XYZ$
Criterion Used:
Two sides (RP and RQ) and the angle included between them ($\angle R$) in $\triangle PQR$ are equal to the corresponding two sides (ZX and ZY) and the included angle ($\angle Z$) in $\triangle XYZ$. Therefore, the congruence is established by the SAS (Side-Angle-Side) congruence criterion.
(c)
In $\triangle LMN$ and $\triangle GFH$, the following parts are given as equal:
$\angle MLN = \angle FGH$
(Angle) (Given)
$\angle NML = \angle GFH$
(Angle) (Given)
ML = FG
(Side) (Given)
Conclusion: $\triangle LMN \cong \triangle GFH$
Criterion Used:
Two angles ($\angle M$ and $\angle L$) and the side included between them (ML) in $\triangle LMN$ are equal to the corresponding two angles ($\angle F$ and $\angle G$) and the included side (FG) in $\triangle GFH$. Therefore, the congruence is established by the ASA (Angle-Side-Angle) congruence criterion.
(d)
In the right-angled triangles $\triangle ABE$ and $\triangle CDB$, the following parts are given as equal:
EB = DB
(Hypotenuse) (Given)
AE = BC
(Side) (Given)
$\angle A = \angle C = 90^\circ$
(Right angle) (Given)
Conclusion: $\triangle ABE \cong \triangle CDB$
Criterion Used:
The triangles are right-angled, their hypotenuses (EB and DB) are equal, and one pair of corresponding sides (AE and BC) are equal. Therefore, the congruence is established by the RHS (Right angle-Hypotenuse-Side) congruence criterion.
Question 2. You want to show that ∆ART ≅∆PEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR =
(ii) RT =
(iii) AT =
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and
(ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ?
(ii) ?
Answer:
To show that $\triangle ART \cong \triangle PEN$, we use the given congruence correspondence: A ↔ P, R ↔ E, and T ↔ N. This tells us which vertices, sides, and angles correspond to each other.
(a) If you have to use SSS criterion, then you need to show
The SSS (Side-Side-Side) criterion requires all three corresponding sides to be equal. Based on the correspondence A↔P, R↔E, T↔N:
(i) Side AR corresponds to side PE. So, you need to show AR = PE.
(ii) Side RT corresponds to side EN. So, you need to show RT = EN.
(iii) Side AT corresponds to side PN. So, you need to show AT = PN.
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
The SAS (Side-Angle-Side) criterion requires two sides and the included angle to be equal. The angle $\angle T$ is included between sides RT and AT. The corresponding angle $\angle N$ is included between sides EN and PN.
(i) Side RT must be equal to its corresponding side EN. So, you need to have RT = EN.
(ii) Side AT must be equal to its corresponding side PN. So, you need to have PN = AT.
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
The ASA (Angle-Side-Angle) criterion requires two angles and the included side to be equal. The side AT is included between angles $\angle A$ and $\angle T$. The corresponding side PN is included between angles $\angle P$ and $\angle N$.
(i) The angle at vertex A must be equal to the angle at the corresponding vertex P. So, you need to have $\angle A = \angle P$ (or $\angle RAT = \angle EPN$).
(ii) The angle at vertex T must be equal to the angle at the corresponding vertex N. So, you need to have $\angle T = \angle N$ (or $\angle RTA = \angle ENP$).
Question 3. You have to show that ∆AMP ≅ ∆AMQ.
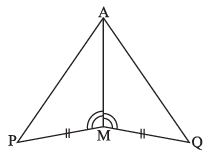
In the following proof, supply the missing reasons.
| Steps | Reasons |
|---|---|
| (i) PM = QM | (i) ... |
| (ii) ∠PMA = ∠QMA | (ii) ... |
| (iii) AM = AM | (iii) ... |
| (iv) ∆AMP ≅ ∆AMQ | (iv) ... |
Answer:
Here is the completed proof with the correct reasons supplied:
| Steps | Reasons |
| (i) PM = QM | (i) Given (This is indicated by the tick marks on the figure.) |
| (ii) ∠PMA = ∠QMA | (ii) Given (This is indicated by the angle marks on the figure.) |
| (iii) AM = AM | (iii) Common side (The side AM is part of both triangles.) |
| (iv) ∆AMP ≅ ∆AMQ | (iv) SAS (Side-Angle-Side) congruence criterion (Using the equal parts from steps (i), (ii), and (iii).) |
Question 4.
In ∆ABC, ∠A = 30° , ∠B = 40° and ∠C = 110°
In ∆PQR, ∠P = 30° , ∠Q = 40° and ∠R = 110°
A student says that ∆ABC ≅∆PQR by AAA congruence criterion. Is he justified? Why or why not?
Answer:
No, the student is not justified in his claim.
Reason:
The core reason is that there is no AAA (Angle-Angle-Angle) congruence criterion in geometry. For two triangles to be congruent, they must have the same size and the same shape. While having all three corresponding angles equal ensures that the triangles have the same shape, it does not guarantee that they are the same size.
Having all three corresponding angles equal only proves that the triangles are similar, not congruent.
Why AAA is not a congruence rule:
To be congruent, all corresponding sides must also be equal. The AAA condition does not provide any information about the lengths of the sides. We can easily draw two triangles with the same angles but different side lengths.
For example, an equilateral triangle with sides of 5 cm has all angles equal to $60^\circ$. Another equilateral triangle with sides of 10 cm also has all angles equal to $60^\circ$. They have the same shape (AAA), but they are not the same size and therefore are not congruent.
Therefore, to prove congruence, we must use one of the established criteria (SSS, SAS, ASA, or RHS), all of which require at least one pair of corresponding sides to be equal.
Question 5. In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ∆RAT ≅ ?
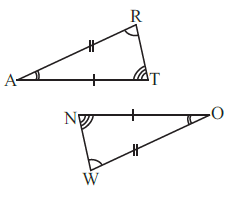
Answer:
Given:
The two triangles shown in the figure are congruent. The corresponding parts are indicated by markings on the sides and angles.
To Find:
The correct congruence statement that completes the relation $\triangle RAT \cong$ ?
Solution:
To establish the correct congruence relation, we must determine the correspondence between the vertices of the two triangles. We do this by matching the parts that have identical markings.
Upon inspection, there is a contradiction between the angle markings and the side markings. We will proceed by establishing the correspondence based on the side markings as this leads to a consistent result.
1. Matching the Vertices:
First, we identify a unique vertex. Vertex A in $\triangle RAT$ is the point where the side with one tick mark (AT) and the side with two tick marks (AR) meet.
In the other triangle, vertex O is the point where the side with one tick mark (ON) and the side with two tick marks (OW) meet.
This means vertex A corresponds to vertex O (A ↔ O).
Next, we match the corresponding sides. The side AR has two tick marks, and the side OW has two tick marks. Since we already know that A corresponds to O, the other endpoint of side AR, which is R, must correspond to the other endpoint of side OW, which is W.
This means vertex R corresponds to vertex W (R ↔ W).
Finally, the side AT has one tick mark, and the side ON has one tick mark. Since A corresponds to O, the endpoint T must correspond to the endpoint N.
This means vertex T corresponds to vertex N (T ↔ N).
So, the complete correspondence is: R ↔ W, A ↔ O, T ↔ N.
2. Writing the Congruence Statement:
We now write the congruence statement by following the order of the vertices in $\triangle RAT$ and their corresponding partners.
The first vertex is R, which corresponds to W.
The second vertex is A, which corresponds to O.
The third vertex is T, which corresponds to N.
Therefore, the correct congruence statement is:
$\triangle RAT \cong \triangle WON$
Question 6. Complete the congruence statement:
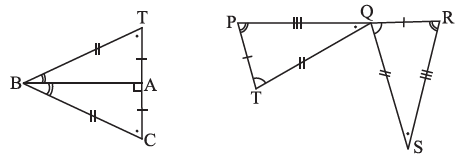
$\triangle BCA \cong \ ?$
$\triangle QRS \cong \ ?$
Answer:
Here are the completed congruence statements based on the given figures.
For the first figure:
Statement: $\triangle BCA \cong \ ?$
Solution:
To find the congruent triangle, we compare the parts of $\triangle BCA$ with the parts of $\triangle BTA$ using the markings in the figure.
1. BC = BT (Given by the double tick marks on the sides).
2. CA = TA (Given by the single tick marks on the sides).
3. BA = BA (This is a common side to both triangles).
Since all three corresponding sides are equal, the triangles are congruent by the SSS (Side-Side-Side) congruence criterion.
The correspondence of the vertices is:
- B corresponds to B (common vertex).
- C corresponds to T (since BC = BT and CA = TA).
- A corresponds to A (common vertex).
Therefore, the complete statement is:
$\triangle BCA \cong \triangle BTA$
For the second figure:
Statement: $\triangle QRS \cong \ ?$
Solution:
We compare the parts of $\triangle QRS$ with the parts of $\triangle TPQ$ using the markings in the figure.
1. QR = TP (Given by the single tick marks on the sides).
2. RS = PQ (Given by the triple tick marks on the sides).
3. SQ = QT (Given by the double tick marks on the sides).
Since all three corresponding sides are equal, the triangles are congruent by the SSS (Side-Side-Side) congruence criterion.
The correspondence of the vertices is:
- Q corresponds to T (vertex between sides with 1 and 2 ticks).
- R corresponds to P (vertex between sides with 1 and 3 ticks).
- S corresponds to Q (vertex between sides with 3 and 2 ticks).
Therefore, the complete statement is:
$\triangle QRS \cong \triangle TPQ$
Question 7. In a squared sheet, draw two triangles of equal areas such that
(i) the triangles are congruent.
(ii) the triangles are not congruent.
What can you say about their perimeters?
Answer:
We can draw the required triangles on a squared sheet (graph paper) by using the grid lines as units of measurement.
(i) Two triangles of equal areas that are congruent.
Drawing:
1. Draw a right-angled triangle, $\triangle ABC$, such that its base BC is 4 units and its height AB is 3 units.
2. Draw another right-angled triangle, $\triangle PQR$, at a different location on the sheet, such that its base QR is 4 units and its height PQ is 3 units.
Analysis:
Area of $\triangle ABC = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 4 \times 3 = 6$ square units.
Area of $\triangle PQR = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 4 \times 3 = 6$ square units.
The areas are equal. Since all corresponding sides are equal (AB=PQ=3, BC=QR=4, and AC=PR=$\sqrt{3^2+4^2}=5$), the triangles are congruent by the SSS criterion.
Perimeters:
Perimeter of $\triangle ABC = 3 + 4 + 5 = 12$ units.
Perimeter of $\triangle PQR = 3 + 4 + 5 = 12$ units.
As expected, their perimeters are equal.
(ii) Two triangles of equal areas that are not congruent.
Drawing:
1. Draw a right-angled triangle, $\triangle XYZ$, with a base YZ of 4 units and a height XY of 3 units. Its area will be 6 square units.
2. Draw another triangle, $\triangle LMN$, with a base MN of 6 units and a height of 2 units. Its area will also be 6 square units, but its shape will be different.
Analysis:
Area of $\triangle XYZ = \frac{1}{2} \times 4 \times 3 = 6$ square units.
Area of $\triangle LMN = \frac{1}{2} \times 6 \times 2 = 6$ square units.
The areas are equal. However, the side lengths of $\triangle XYZ$ are 3, 4, and 5. The side lengths of $\triangle LMN$ (if made a right triangle) would be 2, 6, and $\sqrt{2^2+6^2} = \sqrt{40}$. Since their side lengths are different, the triangles are not congruent.
Perimeters:
Perimeter of $\triangle XYZ = 3 + 4 + 5 = 12$ units.
Perimeter of $\triangle LMN$ (as a right triangle) = $2 + 6 + \sqrt{40} \approx 8 + 6.32 = 14.32$ units.
Their perimeters are not equal.
What can you say about their perimeters?
From the above examples, we can conclude:
1. If two triangles are congruent, they will always have the same area and the same perimeter.
2. If two triangles have the same area but are not congruent, their perimeters are not necessarily equal. In most cases, their perimeters will be different.
Question 8. Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Answer:
Yes, it is possible to draw two triangles that have five pairs of congruent parts but are still not congruent. This happens when the congruence criteria (like SAS or ASA) are not met because the congruent parts do not correspond in the required manner.
Construction Idea:
The key is to construct two triangles that are similar but not congruent. Similar triangles have all three corresponding angles equal, which gives us three pairs of congruent parts. We then need to construct them in such a way that two sides of the first triangle are equal to two sides of the second triangle.
This can be achieved if the side lengths of the first triangle are in a geometric progression (e.g., 4, 6, 9, with a common ratio of 1.5), and the second triangle is a scaled-up version of the first, using that same ratio as the scaling factor.
Rough Sketch and Explanation:
Let's draw two triangles, $\triangle ABC$ and $\triangle PQR$.
1. Let $\triangle ABC$ have side lengths AB = 4 cm, AC = 6 cm, and BC = 9 cm.
2. Let $\triangle PQR$ be similar to $\triangle ABC$ with a scale factor of 1.5. Its corresponding side lengths will be:
PQ = 1.5 $\times$ AB = 1.5 $\times$ 4 = 6 cm
PR = 1.5 $\times$ AC = 1.5 $\times$ 6 = 9 cm
QR = 1.5 $\times$ BC = 1.5 $\times$ 9 = 13.5 cm
Identifying the Five Pairs of Congruent Parts:
By comparing the two triangles we have drawn, we can find five pairs of congruent parts:
Three pairs of angles (because the triangles are similar):
1. $\angle A = \angle P$
2. $\angle B = \angle Q$
3. $\angle C = \angle R$
Two pairs of sides (by coincidence of our chosen numbers):
4. Side AC (length 6 cm) = Side PQ (length 6 cm)
5. Side BC (length 9 cm) = Side PR (length 9 cm)
Why the Triangles are Not Congruent:
Despite having five pairs of congruent parts, the triangles are not congruent because their third pair of sides are not equal:
AB = 4 cm, while the corresponding side QR = 13.5 cm.
Since not all corresponding parts are equal, $\triangle ABC$ is not congruent to $\triangle PQR$.
Question 9. If ∆ABC and ∆PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
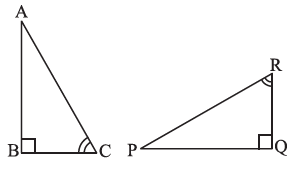
Answer:
Given Information from the Figure:
By observing the markings on the two triangles, we can identify two pairs of congruent parts that are already given:
$\angle B = \angle Q$
(Both are right angles, 90°)
$\angle C = \angle R$
(Indicated by the double arc markings)
Additional Pair of Corresponding Parts Needed:
To make the triangles congruent, we need to add one more pair of corresponding parts to satisfy one of the congruence criteria (like SSS, SAS, ASA, or RHS).
Since we already have two pairs of equal angles, the most direct way to establish congruence is by using the ASA (Angle-Side-Angle) congruence criterion. This rule requires that the side included between the two equal angles must also be equal.
In $\triangle ABC$, the side included between $\angle B$ and $\angle C$ is the side BC.
In $\triangle PQR$, the side included between the corresponding angles $\angle Q$ and $\angle R$ is the side QR.
Therefore, for the ASA criterion to apply, we need to state that these two sides are equal.
The additional pair of corresponding parts needed is:
BC = QR
Criterion Used:
With the additional information that BC = QR, we have:
1. $\angle B = \angle Q$ (Angle)
2. BC = QR (Included Side)
3. $\angle C = \angle R$ (Angle)
This satisfies the conditions for the ASA (Angle-Side-Angle) congruence criterion.
Question 10. Explain, why
∆ABC ≅ ∆FED.
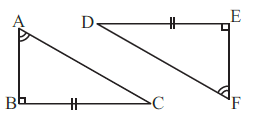
Answer:
To Explain: Why $\triangle ABC \cong \triangle FED$.
Explanation:
First, let's identify the pairs of equal parts that are given in the figure for $\triangle ABC$ and $\triangle FED$.
$\angle A = \angle F$
(Given by the angle markings)
$\angle B = \angle E = 90^\circ$
(Given by the right-angle symbols)
BC = DE
(Given by the side markings)
While we have two angles and a side equal, the side is not included between the angles. So, we cannot directly use the ASA criterion with this information. However, we can use the Angle Sum Property of a triangle to find the third angle.
Using the Angle Sum Property:
For any triangle, the sum of the interior angles is $180^\circ$.
In $\triangle ABC$:
$\angle A + \angle B + \angle C = 180^\circ$
$\angle C = 180^\circ - \angle A - \angle B$
$\angle C = 180^\circ - \angle A - 90^\circ$
... (i)
In $\triangle FED$:
$\angle F + \angle E + \angle D = 180^\circ$
$\angle D = 180^\circ - \angle F - \angle E$
$\angle D = 180^\circ - \angle F - 90^\circ$
... (ii)
Since we are given that $\angle A = \angle F$, the right-hand sides of equations (i) and (ii) are equal. Therefore, the left-hand sides must also be equal.
$\angle C = \angle D$
Applying the ASA Congruence Criterion:
Now, we can prove the congruence using the ASA (Angle-Side-Angle) criterion by considering the side BC and its adjacent angles.
In $\triangle ABC$ and $\triangle FED$:
$\angle B = \angle E$
(Angle)
BC = DE
(Included Side)
$\angle C = \angle D$
(Angle) (Proved above)
Since two angles and the included side of $\triangle ABC$ are equal to the corresponding two angles and included side of $\triangle FED$, the triangles are congruent.
Therefore, by the ASA congruence criterion, $\triangle ABC \cong \triangle FED$.
Alternate Explanation (Using AAS Criterion):
The congruence can also be explained directly by the AAS (Angle-Angle-Side) congruence criterion, which states that if two angles and a non-included side of one triangle are equal to the corresponding two angles and non-included side of another triangle, then the triangles are congruent.
In this case, we have:
$\angle A = \angle F$
(Angle)
$\angle B = \angle E$
(Angle)
BC = DE
(Non-included Side)
Thus, by the AAS criterion, $\triangle ABC \cong \triangle FED$.

